Several ancient arguments suggest a curved Earth, such asthe observation that ships disappear mast-last over thehorizon, andEratosthenes'surprisingly accurate calculation of the size of theEarthby measuring a difference in shadow length betweenAlexandria and Syene. These observations, however, suggestmerely a curved Earth rather than a spherical one.
Another ancient argument specifically suggesting aspherical Earth is the fact that the shadow of the Earth onthe moon during a Lunar eclipse is circular.
My question is: is it true that the sphere isthe only surface all of whose projections are disks?
It surely seems to be true. The corresponding fact,however, is not true in two dimensions. The Reuleauxtrianglepictured below is a figure of constantwidth,meaning that every projection of it in the plane is a linesegment of the same length.
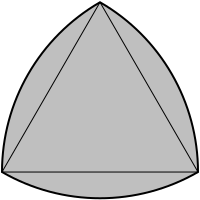
There are also surfaces of constantwidthin higher dimensions, meaning that any two parallelbounding set of hyperplanes (touching the boundary) haveconstant separation. But all of the non-spherical examplesof such surfaces I have seen have obviously non-circularprojections.
It also seems clear that finitely many circular projectionsis insufficient, since intersecting finitely many cylinderswould produce a surface having corners and containing somestraight line segments.
The fact that you can spin such a surface with all circularprojections inside any bounding cylinder is suggestive, but itis also true that you can spin the Reuleaux triangleinside a square,even though it isn't circular.
Further questions would include:
- To what extent are other surfaces determined by theirprojections? That is, which other shapes can we recognizeby the set of their shadows?
- In particular, can we recognize the cube and other regular solids by their shadows?
- Which sets of shadows are realizable as projections of asurface? Is there some way to characterize these sets?Clearly they must be continuously deformable to oneanother and obey several other obvious conditions.
We had a great time discussing the question after our logicseminar here in New York this week, when our speakerMaryanthe Malliaris askedthe spherical Earth question.
December 20, 2010: In light (or dark, as it were) of the lunar eclipse tonight, I am bumping this question, with the remark also that despite the truly outstanding answers we have received, several of the further questions stated above are not fully answered.
